Eine umfassende visuelle Anleitung zu Schiefe/Kurtosis und wie sie sich auf Verteilungen und letztlich auf Ihr Data-Science-Projekt auswirken.

Nachdem Sie Daten gesammelt und Stunden damit verbracht haben, sie zu bereinigen, können Sie endlich mit der Erkundung beginnen! Diese Phase, die oft als Exploratory Data Analysis (EDA) bezeichnet wird, ist vielleicht der wichtigste Schritt in einem Datenprojekt. Die aus der EDA gewonnenen Erkenntnisse wirken sich auf alle nachfolgenden Schritte aus.

Einer der wichtigsten Schritte bei EDA ist beispielsweise die Überprüfung der Verteilungsformen. Die korrekte Identifizierung der Form beeinflusst viele Entscheidungen später im Projekt, beispielsweise:

• Weitere Vorverarbeitungsschritte
• Ob eine Ausreißererkennung und ggf. Entfernung durchgeführt wird
• Feature-Transformation oder Skalierungsschritte
• Merkmalsauswahl
• Algorithmusauswahl

und so weiter. Es gibt zwar visuelle Hilfsmittel, um diese Aufgabe zu erledigen, aber Sie benötigen zuverlässigere Messgrößen, um verschiedene Eigenschaften von Verteilungen zu quantifizieren. Zwei dieser Messgrößen sind Schiefe und Kurtosis . Sie können sie verwenden, um die Ähnlichkeit zwischen Ihren Verteilungen und einer perfekten Normalverteilung zu beurteilen.

Wenn Sie diesen Artikel zu Ende lesen, erfahren Sie im Detail:

• Was sind Schiefe und Kurtosis
• Die Arten von Schiefe und Kurtosis
• Die Auswirkungen von Schiefe und Kurtosis auf Modelle des maschinellen Lernens
• Schiefe und Kurtosis in Python manuell und mit Drittanbieterpaketen berechnen
• Visualisierung von Verteilungen zur Überprüfung von Schiefe- und Kurtosiswerten (umfassender und unterhaltsamer Abschnitt)

Lass uns anfangen!

Was ist Schiefe?

Wir sehen überall eine Normalverteilung: bei menschlichen Körpermaßen, beim Gewicht von Gegenständen, bei IQ-Werten, bei Testergebnissen oder sogar im Fitnessstudio:

Sie ist nicht nur die Lieblingsverteilung der Natur, sondern wird auch von fast allen Algorithmen des maschinellen Lernens allgemein geliebt. Während einige sie zur Verbesserung und Stabilisierung ihrer Leistung nutzen möchten, weigern sich andere schlichtweg, mit etwas anderem als der Normalverteilung zu arbeiten (ich spreche zu euch, linearen Modellen).

Um das Normalitätsbedürfnis der Algorithmen zu erfüllen, benötigen wir eine Möglichkeit, zu messen, wie ähnlich (oder (unähnlich)) unsere eigenen Verteilungen im Vergleich zur perfekten Glockenkurve sind.

Beginnen wir mit den Enden. Bei einer perfekten Normalverteilung sind die Enden gleich lang. Wenn jedoch zwischen den Enden eine Asymmetrie besteht, die der Verteilung ein schiefes, auf eine Seite gequetschtes Aussehen verleiht, sprechen wir von Schiefe. Und Sie ahnen es schon: Wir messen das Ausmaß dieser Asymmetrie mit der Schiefe .

Die korrekte Kategorisierung und Messung der Schiefe liefert Einblicke in die Streuung der Werte um den Mittelwert und beeinflusst die Wahl statistischer Techniken und Datentransformationen. Beispielsweise könnten stark schiefe Verteilungen von Normalisierungs- oder Skalierungstechniken profitieren, um sie einer Normalverteilung ähnlich zu machen. Dies würde die Modellleistung verbessern.

Arten der Schiefe

Es gibt drei Arten von Schiefe: positive, negative und Null-Schiefe.

Beginnen wir mit dem letzten. Eine Verteilung mit Nullschiefe hat die folgenden Eigenschaften:

• Symmetrische Verteilung mit gleichmäßig um den Mittelwert zentrierten Werten.
• Keine Schieflage, Neigung oder Ausreißer zu beiden Seiten.
• Mittelwert, Median und Modus liegen alle im Mittelpunkt.

In der Praxis bilden Mittelwert, Median und Modus möglicherweise keine perfekt überlappende gerade Linie. Sie können leicht voneinander abweichen, aber der Unterschied wäre zu gering, um eine Rolle zu spielen.

Bei einer Verteilung mit positiver Schiefe (rechtsschief):

• Der rechte Rand der Verteilung ist länger oder dicker als der linke.
• Der Mittelwert ist größer als der Median und der Modus ist kleiner als sowohl Mittelwert als auch Median.
• Niedrigere Werte konzentrieren sich auf dem „Hügel“ der Verteilung, während Extremwerte sich im langen rechten Schwanz befinden.
• Sie wird auch als rechtsschiefe Verteilung bezeichnet.

Bei einer Verteilung mit negativer Schiefe (linksschief):

• Der linke Rand der Verteilung ist länger oder dicker als der rechte.
• Der Mittelwert ist kleiner als der Median und der Modus ist größer als Mittelwert und Median.
• Höhere Werte konzentrieren sich auf dem „Hügel“ der Verteilung, während Extremwerte sich im langen linken Schwanz befinden.
• Sie wird auch als linksschiefe Verteilung bezeichnet.

Um sich die Unterschiede zwischen positiver und negativer Schiefe zu merken, stellen Sie sich das folgendermaßen vor: Wenn Sie den Mittelwert einer Verteilung erhöhen möchten, sollten Sie der Verteilung viel höhere Werte als den Mittelwert hinzufügen. Um den Mittelwert zu senken, sollten Sie das Gegenteil tun – der Verteilung viel niedrigere Werte als den Mittelwert hinzufügen. Wenn also die Mehrheit der Extremwerte höher als der Mittelwert ist, ist die Schiefe positiv, weil sie den Mittelwert erhöhen. Wenn die Mehrheit der Extremwerte kleiner als der Mittelwert ist, ist die Schiefe negativ, weil sie den Mittelwert senken.

So berechnen Sie die Schiefe in Python

Es gibt viele Möglichkeiten, die Schiefe zu berechnen, aber die einfachste ist der zweite Schiefekoeffizient nach Pearson, auch als mittlere Schiefe bekannt.

Lassen Sie uns die Formel manuell in Python implementieren:

Eine weitere Formel, die stark von den Arbeiten Karl Pearsons beeinflusst ist, ist die momentbasierte Formel zur Approximation der Schiefe. Sie ist zuverlässiger und wird wie folgt angegeben:

Hier:

• n stellt die Anzahl der Werte in einer Verteilung dar
• x_i bezeichnet jeden Datenpunkt

Lassen Sie es uns auch in Python implementieren:

Wenn Sie die Schiefe nicht manuell berechnen möchten (wie ich), können Sie integrierte Methoden von pandasoder verwenden scipy:

Obwohl alle Formeln zur Schätzung der Schiefe unterschiedliche Werte liefern, sind die Unterschiede zu gering, um signifikant zu sein oder die Kategorisierung der Schiefe zu ändern. Beispielsweise nutzen alle Methoden, die wir heute verwendet haben, im Hintergrund unterschiedliche Formeln, aber die Ergebnisse liegen sehr nahe beieinander.

Nachdem Sie die Schiefe berechnet haben, können Sie das Ausmaß der Schiefe kategorisieren:

• (-0,5, 0,5) – niedrig oder ungefähr symmetrisch.
• (-1, -0,5) U (0,5, 1) – mäßig schief.
• Über -1 und 1 – Stark verzerrt.

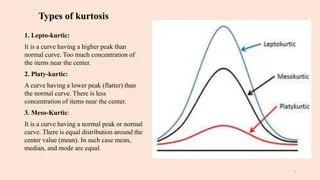
Was ist Kurtosis und welche Arten gibt es?

Während sich die Schiefe auf die Streuung (die Enden) der Normalverteilung konzentriert, konzentriert sich die Kurtosis mehr auf die Höhe. Sie sagt uns, wie spitz oder flach unsere Normalverteilung (oder normalähnliche Verteilung) ist . Der Begriff, der aus dem Griechischen kommt und „gekrümmt“ oder „gewölbt“ bedeutet, wurde erstmals, wenig überraschend, vom britischen Mathematiker Karl Pearson geprägt (er verbrachte sein Leben mit dem Studium von Wahrscheinlichkeitsverteilungen).

Eine hohe Kurtosis deutet auf Folgendes hin:

• Scharfe Spitze im Zentrum der Verteilung.
• Mehr Werte konzentrieren sich um den Mittelwert als bei der Normalverteilung.
• Schwerere Enden aufgrund einer höheren Konzentration von Extremwerten oder Ausreißern in den Enden.
• Höhere Wahrscheinlichkeit extremer Ereignisse.

Eine niedrige Kurtosis hingegen deutet auf Folgendes hin:

• Flacher Gipfel.
• Es konzentrieren sich zwar weniger Werte um den Mittelwert, aber immer noch mehr als bei der Normalverteilung.
• Hellere Schwänze.
• Geringere Wahrscheinlichkeit extremer Ereignisse.

Je nach Grad weisen Verteilungen drei Arten von Kurtosis auf:

1. Mesokurtische Verteilung (Kurtosis = 3, überschüssige Kurtosis = 0): perfekte Normalverteilung oder sehr nahe daran.
2. Leptokurtische Verteilung (Kurtosis > 3, Exzess-Kurtosis > 0): scharfe Spitze, schwere Enden
3. Platykurtische Verteilung (Kurtosis < 3, Exzess-Kurtosis < 0): flache Spitze, helle Enden

Beachten Sie, dass hier die übermäßige Kurtosis als Kurtosis – 3 definiert wird, wobei die Kurtosis der Normalverteilung als 0 behandelt wird. Auf diese Weise sind die Kurtosis-Werte leichter interpretierbar.

So berechnen Sie Kurtosis in Python

Sie können die Kurtosis in Python auf die gleiche Weise wie die Schiefe mit Pandas oder SciPy berechnen:

Pandas bietet zwei Funktionen für Kurtosis: kurtund kurtosis. Die erste ist exklusiv für Pandas Series, während Sie die andere auf DataFrames verwenden können.

Auch hier unterscheiden sich die Zahlen für die Verteilung, da Pandas und SciPy unterschiedliche Formeln verwenden.

Wenn Sie die Kurtosis manuell berechnen möchten, können Sie die folgende Formel verwenden:

Hier:

• n stellt die Anzahl der Beobachtungen im Datensatz dar
• x_i bezeichnet jeden einzelnen Datenpunkt

Wir werden die Formel wieder innerhalb einer Funktion implementieren:

Und wir finden heraus, dass die Diamantpreise eine Exzesskurtosis von 2,18 haben, was bedeutet, dass die Verteilung, wenn wir sie aufzeichnen, einen schärferen Peak aufweist als eine Normalverteilung.

Also, lasst es uns tun!

Visualisieren von Schiefe und Kurtosis in Python

Eine der besten Möglichkeiten, die Form und damit auch die Schiefe und Kurtosis von Verteilungen zu erkennen, ist ein Kernel Density Estimate (KDE)-Diagramm . Es ist über Seaborn verfügbar:

Dieses Diagramm steht im Einklang mit den Zahlen, die wir bisher gesehen haben: Die Verteilung weist einen langen rechten Schwanz auf, was auf eine positive Schiefe hinweist, und sie weist eine sehr scharfe Spitze auf, die einer hohen Kurtosis entspricht.

KDE ist nicht die einzige Darstellung, in der die Form zu sehen ist. Wir können auch Histogramme verwenden:

Der Nachteil von Histogrammen besteht darin, dass Sie die Anzahl der Bins (die Anzahl der Balken) selbst wählen müssen. Hier gibt es zu viele Balken, die im Bild Rauschen erzeugen – wir können die Form nicht klar definieren. Verringern wir also die Anzahl der Bins:

Jetzt ist die Form besser definiert, aber wir können sie noch verbessern. Indem wir kde=Trueinnerhalb setzen histplot, können wir über den Balken ein KDE der Verteilung zeichnen:

Die überlagerte KDE-Linie sieht gezackt aus und hat nicht die glatte Kurve, die uns die allgemeine Form erkennen lässt. Der Grund für die Zackigkeit ist, dass die Karatverteilung natürlich spitz zuläuft und weit von der Normalverteilung abweicht.

Wir können jedoch die Empfindlichkeit von KDE gegenüber diesen Schwankungen verringern, indem wir die Bandbreite anpassen. Dies geschieht mit dem bw_adjustParameter, der standardmäßig auf 1 eingestellt ist:

Diese Version weist deutlich weniger Stippen auf als das darübergelegte KDE-Diagramm. Um die KDE-Bandbreite anzupassen, wenn Sie ein mit einem KDE überlagertes Histogramm verwenden, können Sie den kde_kwsParameter verwenden:

kde_kwsakzeptiert alle Parameter, die von der Funktion akzeptiert werden kdeplot, die die KDE-Berechnung steuert.

Ein Trick, den Sie beim Plotten von KDEs anwenden können, besteht darin, alles außer der KDE-Linie zu entfernen. Da der Hauptzweck eines KDE darin besteht, die Verteilungsform zu sehen, sind andere Details des Plots wie die Achsenmarkierungen, die Stacheln und Beschriftungen manchmal unnötig:

Dieses Diagramm ist viel übersichtlicher. Sie können das Diagramm weiter verbessern, indem Sie Linien hinzufügen, um die Position von Mittelwert, Median und Modus anzuzeigen:

Dieses Diagramm bestätigt, was wir im Abschnitt zu den Arten der Schiefe besprochen haben: Bei einer positiv schiefen Verteilung ist der Mittelwert höher als der Median und der Modus niedriger als sowohl Mittelwert als auch Median CGI.

Fazit

Schiefe und Kurtosis werden bei der explorativen Datenanalyse oft übersehen, geben aber wichtige Aufschlüsse über die Natur von Verteilungen.

Die Schiefe weist auf eine Neigung der Daten hin, egal ob sie nach links oder rechts tendieren, und offenbart so ihre Asymmetrie (sofern vorhanden). Eine positive Schiefe bedeutet, dass der Schwanz nach rechts zeigt, während eine negative Schiefe in die entgegengesetzte Richtung geht.

Bei Kurtosis dreht sich alles um Spitzen und Enden. Eine hohe Kurtosis schärft Spitzen und belastet Enden, während eine niedrige Kurtosis Daten verteilt und Enden leichter macht.

Wenn Sie mehr über Schiefe und Kurtosis erfahren möchten, können Sie sich diese hervorragenden Kurse zur quantitativen Analyse ansehen, die von Branchenexperten auf DataCamp angeboten werden: